

View Available Hint(s) ΑΣΦ dm = Submit Part C What is the angular speed of the rod at time t? Express your answer in terms of the variables a and t. If an element has length dx, what is the mass of the element? Express your answer in terms of the variables M, L, and dx. Part B To calculate the moment of inertia of the rod, you'll have to divide the rod into infinitesimal elements of mass. View Available Hint(s) h: the distance from 0 to the end of the rod L: the length of the rod O a: the angular acceleration around O OI: the moment of inertia about an axis through O w the angular speed at timet Figure < 1 of 1 ✓t: time OK: the kinetic energy the rod at time OW: the work done on the rod in time t Axis OM: the mass of the rod Mass element: rod segment of length dx ds O a: the linear acceleration of the point farthest from the axis M Submit Previous Answers o Since the rod is uniform, the mass varies linearly with distance. Hence, we have to force a dx into the equation for moment of inertia.
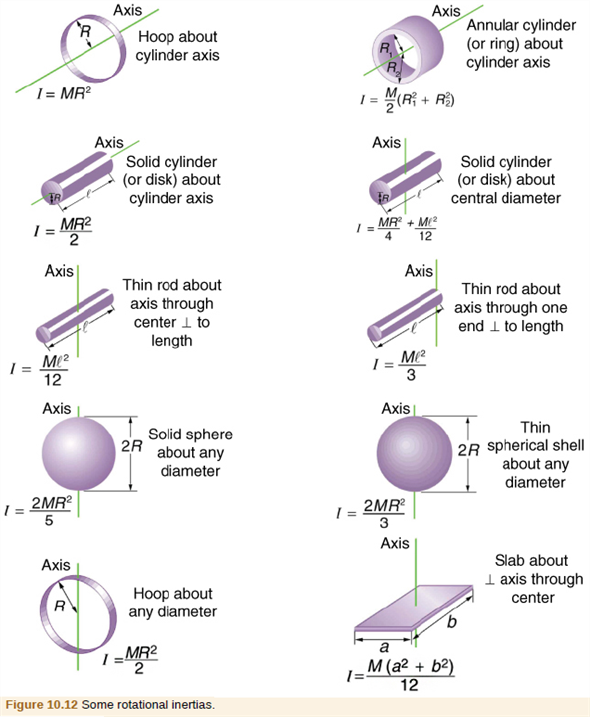
Hey, there is a dm in the equation Recall that we’re using x to sum. (c) At time t, what is the linear acceleration of the point on the rod farthest from the axis? Part A Select the target variables for this problem. Now, we show our formula for the calculation for moment of inertia first: dI dm x2 d I d m x 2. Find how much work is done on the rod in a time t. It is given a constant angular acceleration of magnitude a around the axis through O. Still the torque with respect to point is zero and the previous angular momentum is conserved. (a) Use integration to compute its moment of inertia about an axis through O, at an arbitrary distance h from one end. It might be a baton held by a twirler in a marching band (without the rubber end caps). a) Use the parallel-axis theorem to determine the moment of inertia tensor relative to the end of the rod in terms of the principal axes. The principal axes and the corre- sponding principal-axis moments of inertia relative to the center of mass are shown in Figure. Express the result in terms of the rod's total mass m. The rod's density P and cross-sectional area A are constant. Using integration to determine the moment of inertia for the slender rod. (Figure 1) shows a slender uniform rod with mass M and length L. Question: Consider a slender rod with mass m and length &. This problem has been solved You'll get a detailed solution from a subject matter expert that helps you learn core concepts.


 0 kommentar(er)
0 kommentar(er)
